Formel am Oktaeder
Zur Unterstützung der Lehrbuchaufgabe im Lambacher-Schweizer, Band 3, Seite 87 / Aufgabe 2 (Ausgabe Baden-Württemberg), 1. Auflage, Ernst Klett Verlag GmbH, Stuttgart 2005.
Das Oktaeder ist einer der fünf platonischen Körper.
Aufbau eines Oktaeders
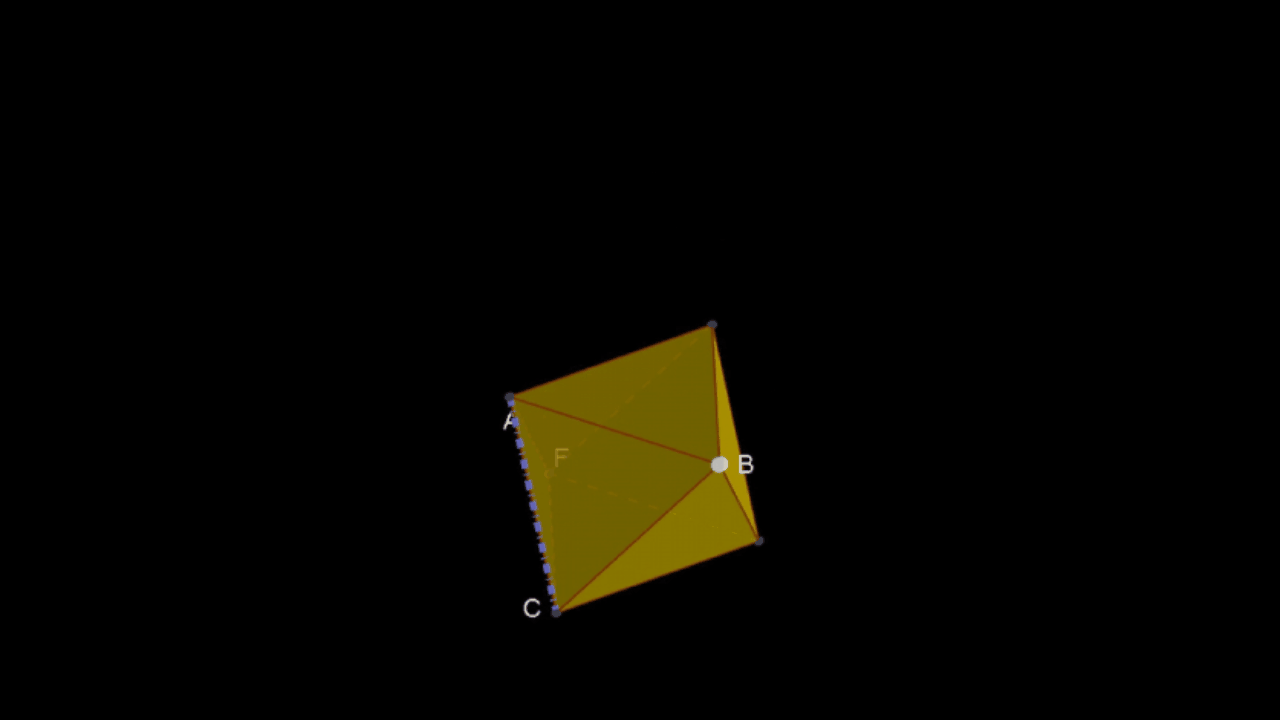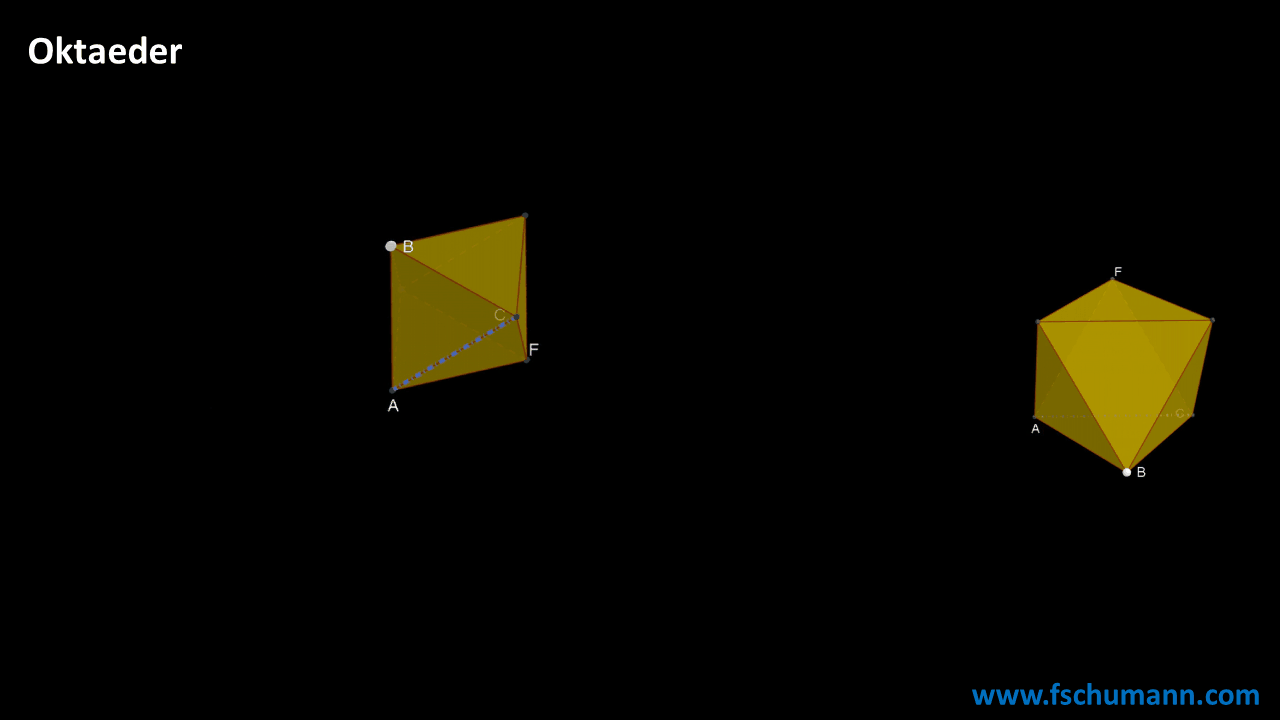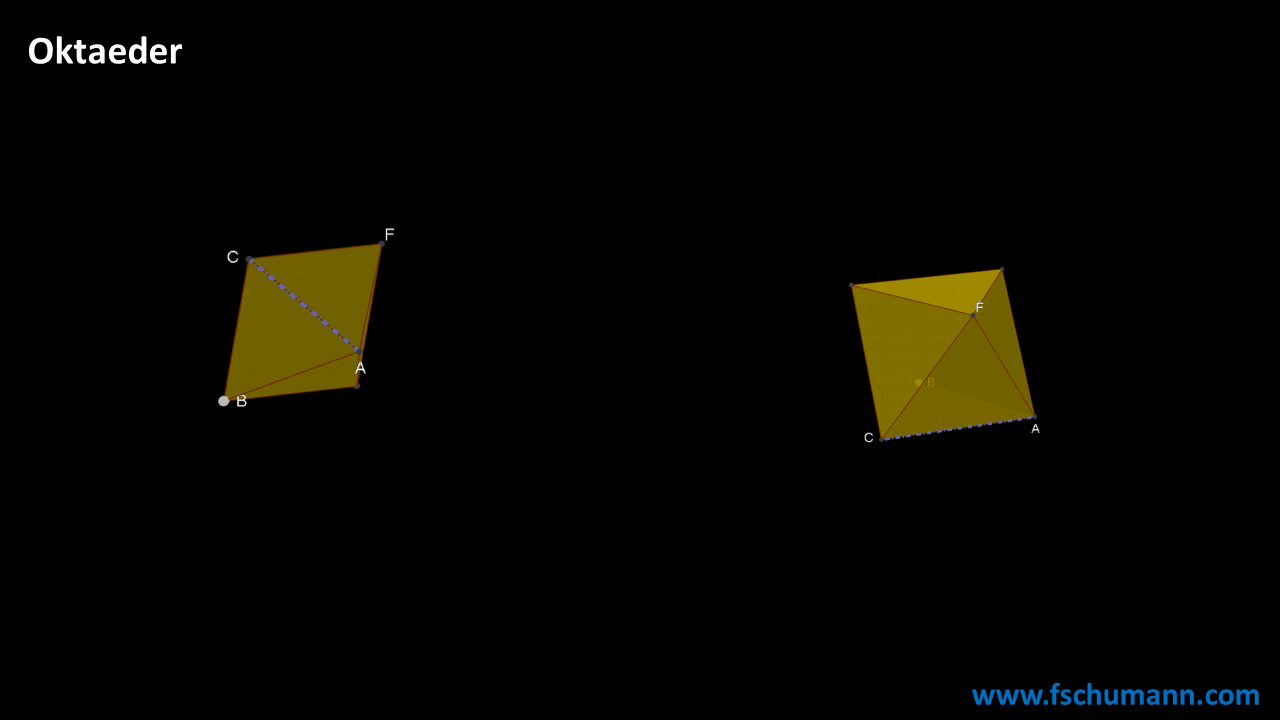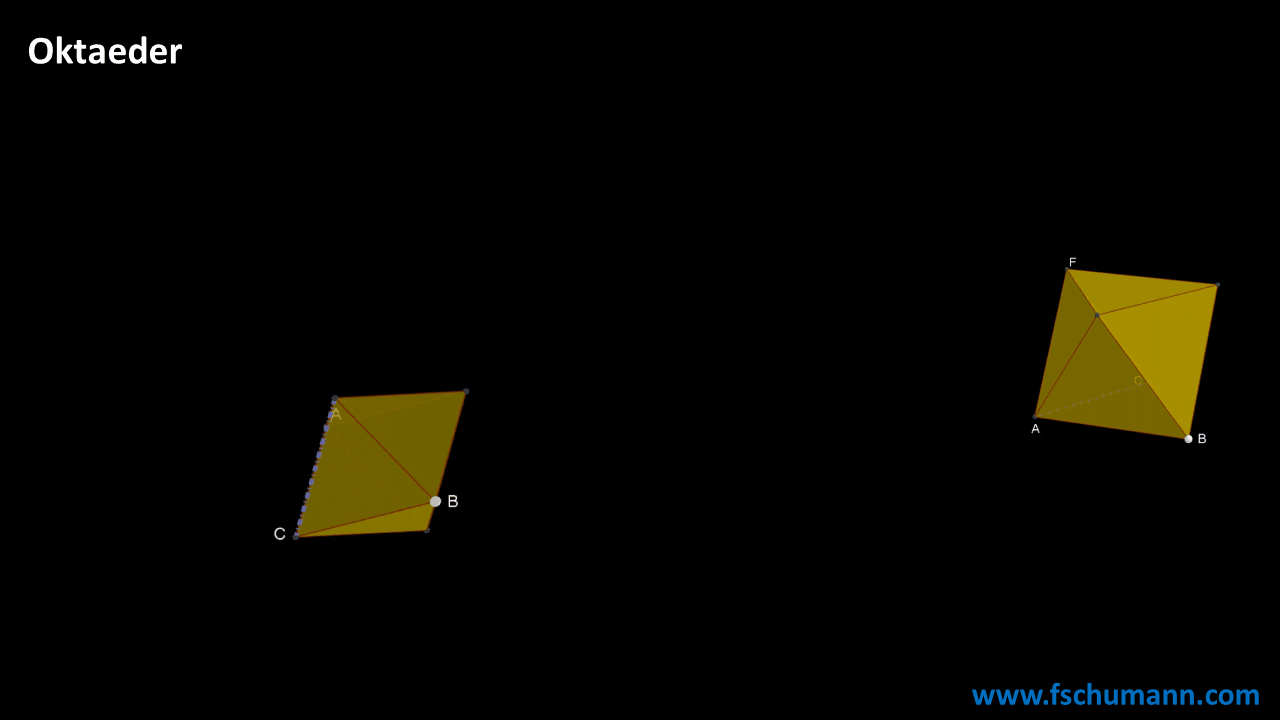
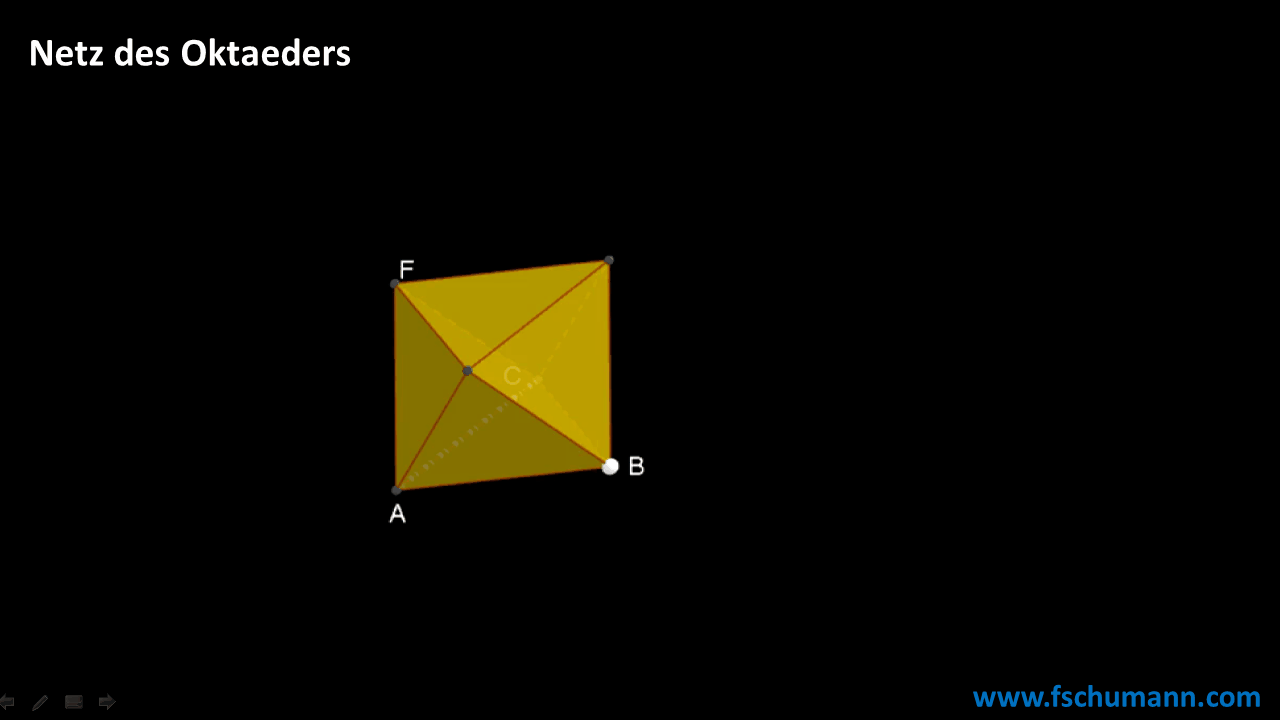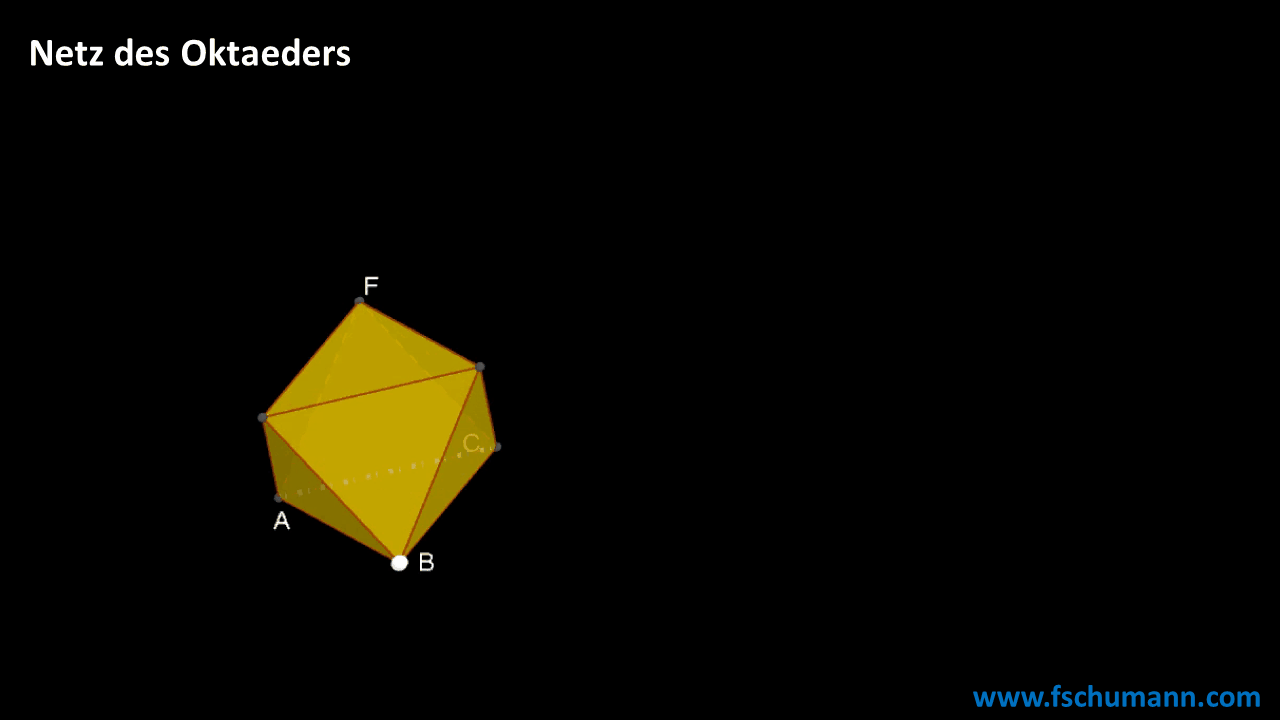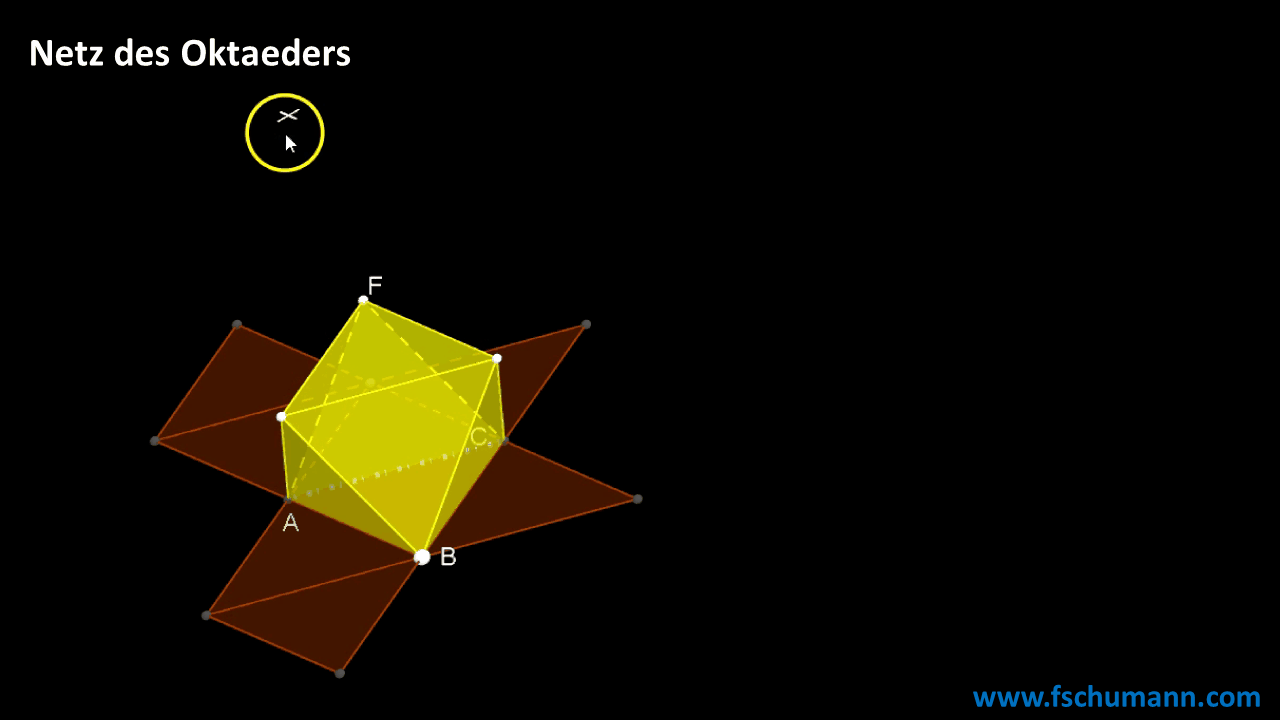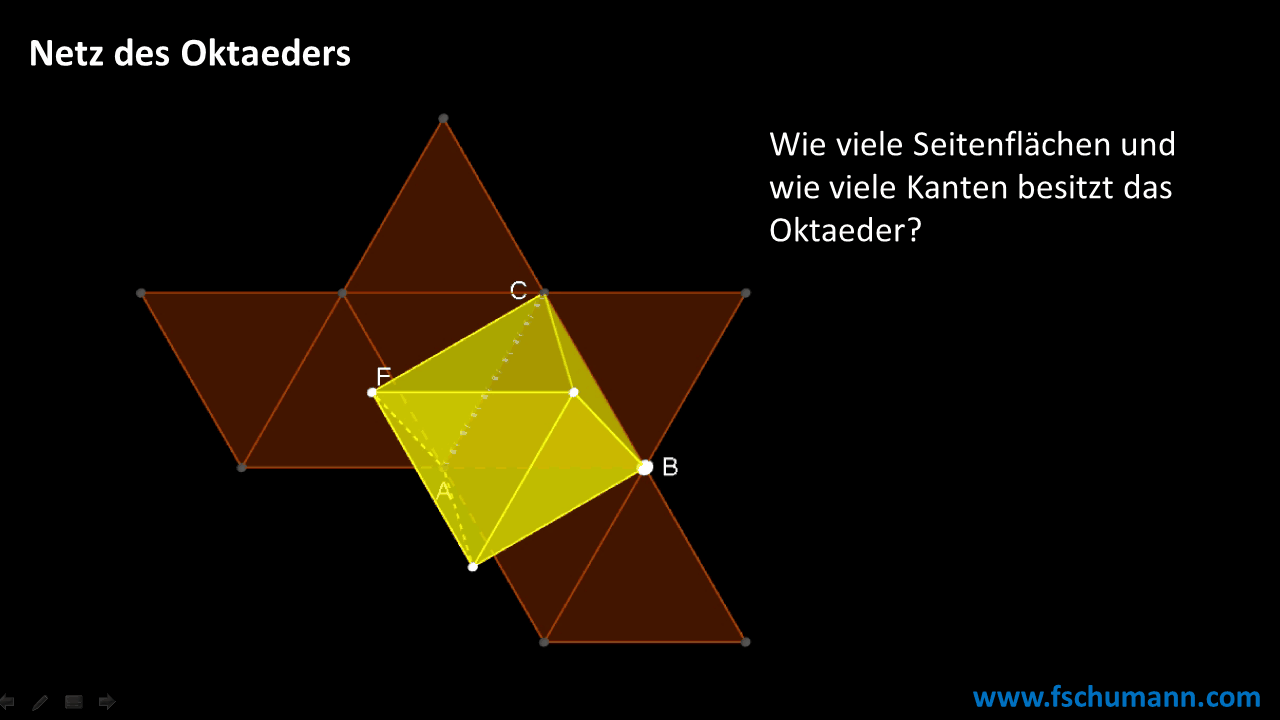
Mit einer Formel rechnen
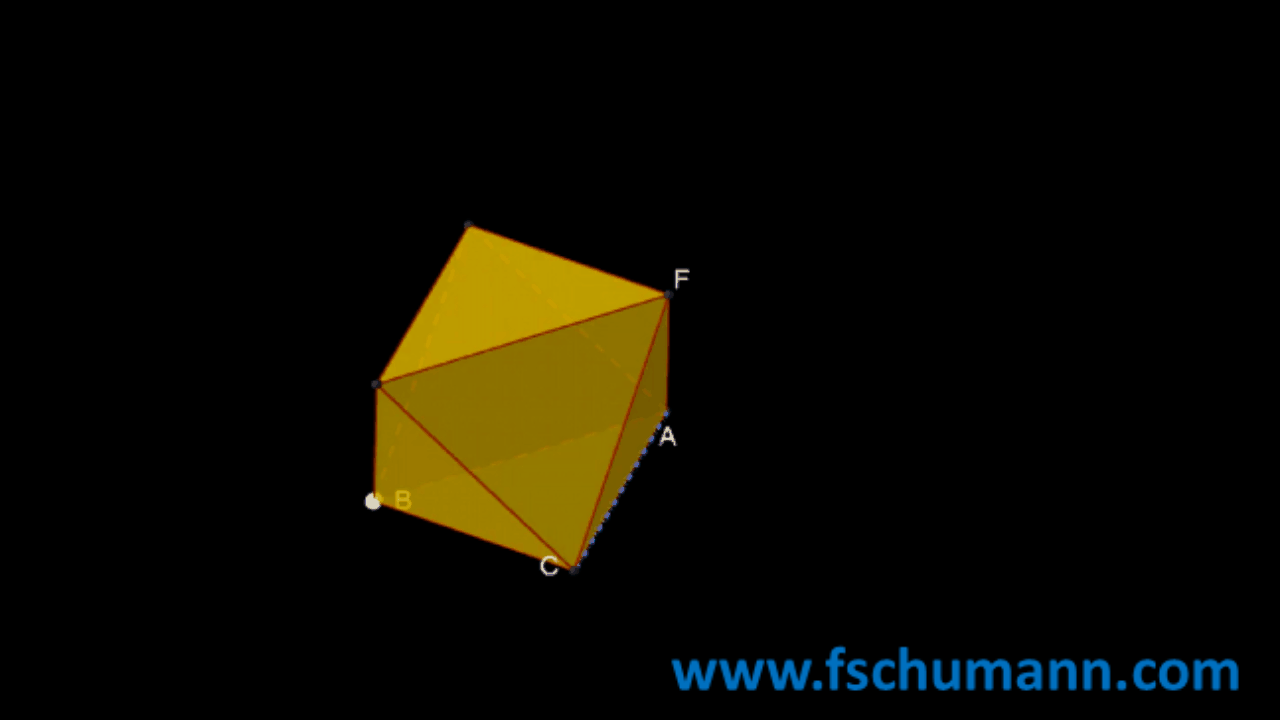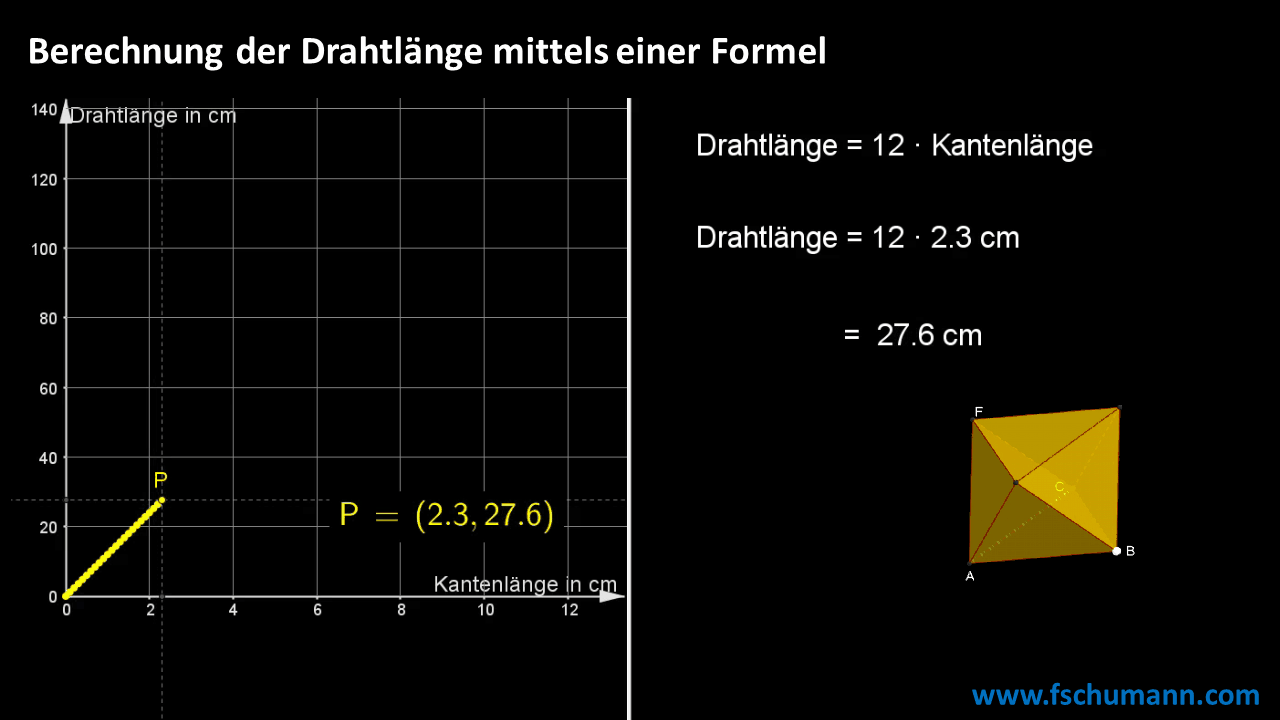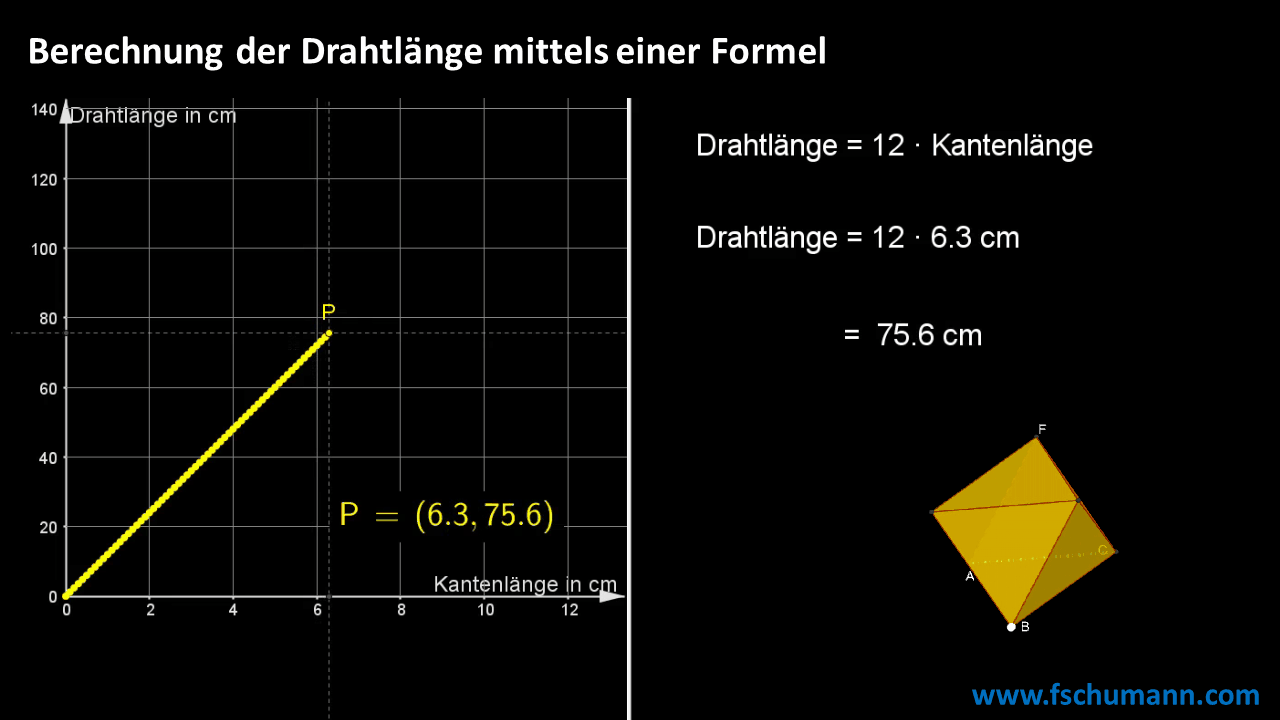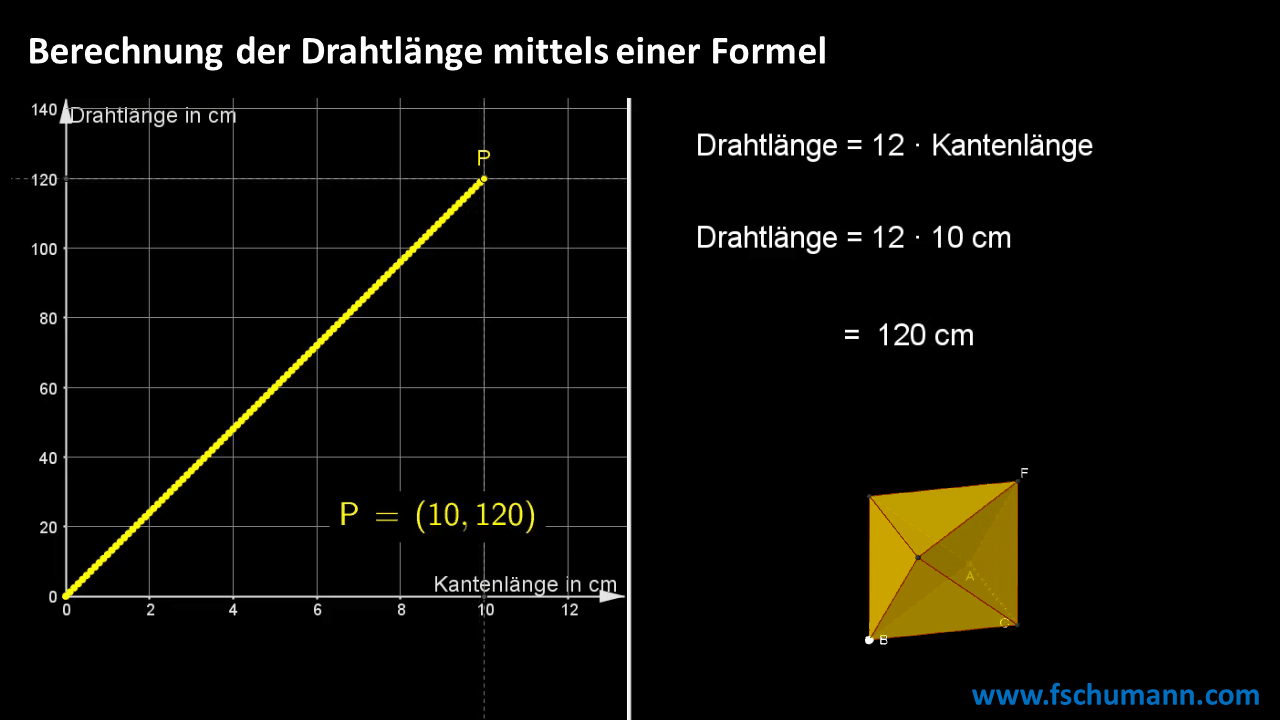
Wenn Du mehr über platonische Köper erfahren möchtest, dann empfehle ich dir das Video Mathematik zum Anfassen – Platonische Körper mit Prof. Dr. Albrecht Beutelspacher auf ARD alpha oder auf YouTube.COM.
© Frank Schumann 2016
